Have you ever considered how we train machine learning models that could mirror our biases? As a seasoned data analyst, I frequently confront this problem. We desire objective systems yet inadvertently impose our preconceived notions of what patterns or 'ideal' data should look like. It highlights the strengths and limitations of techniques like Linear Discriminant Analysis (LDA).
LDA excels in classifying well-defined groups, but what if our chosen features perpetuate hidden bias? Take image analysis: Algorithms focused on standardized visual norms could perpetuate existing inequalities or fail to uncover nuanced insights. Could different data selection, pre-processing, and alternative classification models lead to more equitable, accurate results?
Table of Contents
In this article, we explore LDA in the context of these intriguing questions. Rather than offering a simple tutorial, I'll critically examine its capabilities and how it differs from other classification methods. The goal is to encourage mindful usage of these powerful tools to minimize unintentional bias and ensure outcomes truly reflect the underlying data.
Key Takeaways
- Machine learning algorithms can inherit human biases. Data selection and feature engineering must be done with conscious awareness to avoid unintentionally perpetuating inequalities.
- LDA excels with well-defined groups but is sensitive to feature bias. Understanding when your chosen features may contain underlying biases is crucial for equitable outcomes.
- Comparing multiple classification models provides a more robust solution. No single algorithm is best for every situation. Experimentation reveals strengths and weaknesses for specific datasets.
- KNN, SVM, Logistic Regression, Naive Bayes, and PCA each have their niche. They offer trade-offs in terms of simplicity, handling high dimensions, linearity, computational cost, and feature independence.
- Critical assessment is vital, not just implementation. The article promotes being mindful of algorithm capabilities and assumptions to address the problem effectively.
- The choice of method impacts interpretability and bias reduction. Algorithm selection isn't merely about raw accuracy but how its decisions can be explained and whether they reflect the data fairly.
Linear discriminant analysis is not the only method that can be used for classification and dimensionality reduction. Different machine learning algorithms each have their advantages and disadvantages. Their performance might be better or worse depending on the data and problem. Read more about Concepts, assumptions of LDA, and how to perform LDA in R.
Comparison of LDA with other Machine learning algorithms
| Algorithm | Type | Pros | Cons |
|---|---|---|---|
| Linear Discriminant Analysis (LDA) | Supervised Learning | - Assumes normal distribution of features - Maximizes class separation - Good for multi-class classification | - Sensitive to outliers - Assumes linear decision boundaries - Requires feature independence |
| K-Nearest Neighbors (KNN) | Instance-Based Learning | - Simple to implement - No training phase - Non-parametric - Effective with small datasets | - Computationally expensive during testing - Sensitive to irrelevant features - Needs careful selection of K |
| Support Vector Machines (SVM) | Supervised Learning | - Effective in high-dimensional spaces - Works well with small to medium-sized datasets - Versatile kernels | - Memory-intensive for large datasets - Not suitable for large datasets with lots of noise and overlapping classes |
| Logistic Regression | Supervised Learning | - Outputs probabilities - Efficient for linearly separable data - Interpretable coefficients | - Assumes linear decision boundaries - Prone to overfitting with high-dimensional data |
| Naive Bayes | Supervised Learning | - Simple and efficient - Performs well with small datasets - Handles high-dimensional data well | - Assumes feature independence - Sensitive to irrelevant features - Often oversimplified assumptions |
| Principal Component Analysis (PCA) | Unsupervised Learning | - Reduces dimensionality - Identifies patterns in data - Removes correlations between features | Despite their application in various machine learning algorithms, the cross-validation technique may not maintain the interpretability of features and also assumes linear relationships between variables. |
Comparison of Supervised and Unsupervised Learning Models
Required Packages
- MASS: Supplies fundamental statistical tools for model fitting, including Linear Discriminant Analysis (LDA) methods.
- caret: Serves as a comprehensive framework for model development, offering functions for data preparation, feature tuning, algorithm selection, and performance evaluation.
- pROC: Provides a variety of methods for visualizing and analyzing classification model performance, including ROC curves and AUC calculations.
- irr: Focuses on evaluating inter-rater reliability, a measurement essential to certain classification tasks where multiple human coders/annotators are used to label data.
# Required Packages library(MASS) library(caret) library(pROC) library(irr)
Data Preprocessing
# Set the seed for reproducibility
set.seed(123)
# Split the data into training and testing sets
train_index <- createDataPartition(iris$Species, p = 0.8, list = FALSE)
train <- iris[train_index, ]
test <- iris[-train_index, ]Linear Discriminant Analysis
# Fit the LDA model
LDA <- lda(Species ~ ., data = train)
# Print the model
print(LDA) K-nearest Neighbors (KNN)
K-nearest neighbors (KNN) is a simple and intuitive method that classifies a new observation based on the majority vote of its k-nearest neighbors in the feature space. Using the caret package's train function, we will implement and evaluate KNN for the given classification problem, training and fine-tuning the model with varying methods and parameters. The train function takes a:
- In the classification problem, a formula argument specifies the class variable and the features.
- a data argument, which specifies the data frame,
- a method argument, which specifies the method to use,
- a metric argument, which specifies the metric to optimize,
- a trControl argument, which specifies the resampling method and number of folds,
- a tuneGrid argument, which specifies the grid of tuning parameters.
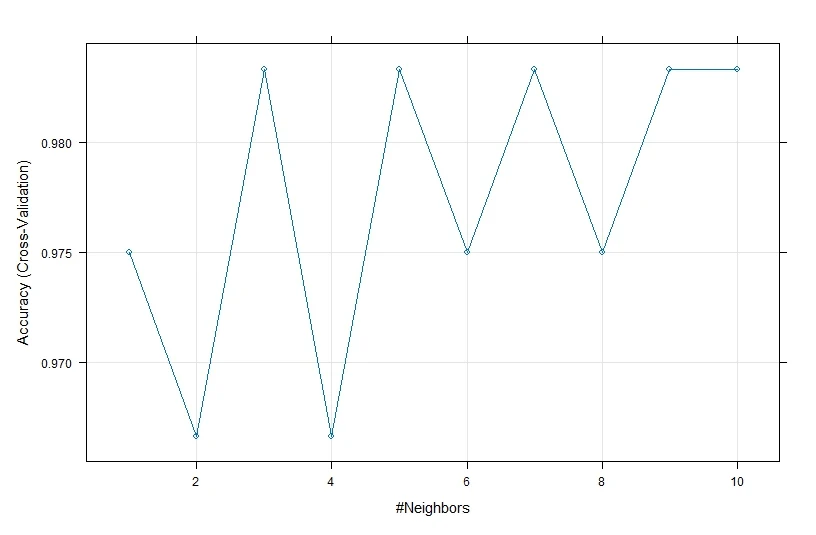
We will use the same formula and data arguments as before, and we will use “knn” as the method argument, “Accuracy” as the metric argument, “cv” as the resampling method, 10 as the number of folds, and a sequence of values from 1 to 10 as the tuning parameter for k. We will assign the output of the train function to a variable called model_knn and then print and plot the model using the print and plot functions.
# Fit the KNN model model_knn <- train(Species ~ ., data = train, method = "knn", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = data.frame(k = 1:10)) print(model_knn) # Plot the model plot(model_knn)

From the output, we can see that the KNN model has an accuracy of greater than 95.83% across different values of k and that the optimal value of k is 1, which means that the model uses only the nearest neighbor to classify a new observation.
Support Vector Machines (SVM)
Support vector machines (SVM) is a powerful and flexible method that classifies a new observation based on the optimal hyperplane that separates the classes in the feature space. To implement and evaluate SVM, we will use the train function from the caret package, with the same arguments as before, except for the method and tuneGrid arguments.
We will use “svmLinear” as the method argument, which specifies the linear kernel for SVM, and a sequence of values from 0.01 to 1 as the tuning parameter for the cost of constraints violation. Using the train function, we will assign the output to a variable named model_svm for the classification problem, then print and plot the model using the print and plot functions to see how features and classes correlate.
# Fit the SVM model model_svm <- train(Species ~ ., data = train, method = "svmLinear", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = data.frame(C = seq(0.01, 1, by = 0.01))) # Print the model print(model_svm) # Plot the model plot(model_svm)

Naive Bayes
Naive Bayes is a simple and fast method that applies Bayes' theorem to classify a new observation based on the conditional probabilities of the features given the class. Naive Bayes assumes that the features are independent of each other given the class, which is often not true in real-world data, but it still works well in many cases.
To implement and evaluate naive Bayes, we will use the `train` function from the `caret` package, with the same arguments as before, except for the method and tuneGrid arguments. We will use "nb" as the method argument, which specifies the naive Bayes model, and NULL as the tuneGrid argument, meaning there are no tuning parameters for this method. We will assign the output of the `train` function to a variable called `model_nb`, then print and plot the model using the `print` and `plot` functions.
# Fit the naive Bayes model model_nb <- train(Species ~ ., data = train, method = "nb", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = NULL) # Print the model print(model_nb) # Plot the model plot(model_nb)
From the output, we can see that the naive Bayes model has an accuracy of 96.67% and a kappa of 0.95, the same as the linear discriminant analysis and the KNN models. We can also see the prediction accuracy plotted against the Laplace smoothing parameter, showing that the accuracy does not alter significantly as the smoothing parameter increases. This suggests that the naive Bayes model is robust to the choice of the smoothing parameter.
Support Vector Machines (SVM)
Support vector machines (SVM) is a powerful and flexible method that classifies a new observation based on the optimal hyperplane that separates the classes in the feature space.
To implement and evaluate SVM, we will use the `train` function from the `caret` package, with the same arguments as before, except for the method and tuneGrid arguments. We will use "svmLinear" as the method argument, which specifies the linear kernel for SVM, and a sequence of values from 0.01 to 1 as the tuning parameter for the cost of constraints violation. We will assign the output of the `train` function to a variable called `model_svm`, and then print and plot the model using the `print` and `plot` functions.
# Fit the SVM model model_svm <- train(Species ~ ., data = train, method = "svmLinear", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = data.frame(C = seq(0.01, 1, by = 0.01))) # Print the model print(model_svm) # Plot the model plot(model_svm)

Related Posts
Principal Component Analysis (PCA)
In a bid to manage the number of observations, principal component analysis (PCA) is used as a technique that reduces the data dimensionality by converting features into a fresh set of orthogonal variables called principal components. The principal components capture the maximum variance in the data and are ordered by decreasing importance. PCA can be used for classification and visualization purposes, as it can reveal the underlying structure and patterns of the data. Read more about the assumption, analysis, and visualization of PCA using R.
To implement and evaluate PCA, we will use the `prcomp` function from the `stats` package, which performs PCA using singular value decomposition. The `prcomp` function takes a data argument, which specifies the data frame, a scale argument, which specifies whether to scale the data to unit variance and a center argument, which specifies whether to center the data to zero mean.
We will use the same data argument as before, and we will set both scale and center arguments to TRUE, as it is recommended to standardize the data before applying PCA. We will assign the output of the `prcomp` function to a variable called `pca`, then print and plot the model using the `print` and `plot` functions.
# Perform the PCA pca <- prcomp(train[, -5], scale = TRUE, center = TRUE) # Print the model print(pca) # Plot the model plot(pca)

From the output, we can see that the PCA model has four principal components, each with a different standard deviation and rotation. The standard deviation measures how much the data varies along each principal component, and the rotation measures how much each original feature contributes to each principal component. The first principal component (PC1) explains the most variance in the data, followed by the second (PC2), the third (PC3), and the fourth (PC4).
We can also see the plot of the standard deviation versus the principal components, which shows that the variance decreases as the number of components increases. This plot can help us decide how many components to retain for further analysis.
A common rule of thumb is to keep the components that have a standard deviation above 1 or that explain at least 80% of the cumulative variance. In this case, we can see that the first two components satisfy both criteria, as they have a standard deviation of 1.71 and 0.96 and explain 86.6% and 12.2% of the variance, respectively. Therefore, we can reduce the dimensionality of the data from four features to two components without losing much information.
Decision Trees
Decision trees are a method that splits the data into branches based on the values of the features. Each branch represents a decision rule that leads to a class label or a further split. Decision trees correlate strongly with easy interpretation and can handle both categorical and numerical features.
To implement and evaluate decision trees, we will use the `train` function from the `caret` package, with the same arguments as before, except for the method and tuneGrid arguments. We will use "rpart" as the method argument, which specifies the recursive partitioning algorithm for decision trees and a sequence of values from 1 to 10 as the tuning parameter for the complexity parameter. We will assign the output of the `train` function to a variable called `model_tree,` then print and plot the model using the `print` and `plot` functions.
# Fit the decision tree model model_tree <- train(Species ~ ., data = train, method = "rpart", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = data.frame(cp = seq(0.01, 0.1, by = 0.01))) # Print the model print(model_tree) # Plot the model plot(model_tree)

From the output, we can see that the decision tree model has an accuracy of 94% and a kappa of 0.9125, slightly lower than the previous models. We can also see the plot of the accuracy versus the complexity parameter, which shows that the accuracy does not change much as the complexity parameter increases. This suggests that the decision tree model is robust to the choice of the complexity parameter.
We can also see the plot of the decision tree itself, which shows the decision rules and the class labels at each node. The decision tree has four terminal nodes, which means that it splits the data into four groups based on the values of Petal.Length and Petal.Width. The decision tree is easy to interpret and can classify new observations by following the branches.
Random Forest
Random forest is a method that combines multiple decision trees into an ensemble that can classify a new observation based on the majority vote of the trees. Random forest can handle both categorical and numerical features and can reduce the overfitting problem of single-decision trees.
To implement and evaluate random forest, we will use the `train` function from the `caret` package, with the same arguments as before, except for the method and tuneGrid arguments. We will use "rf" as the method argument, which specifies the random forest algorithm, and a sequence of values from 1 to 10 as the tuning parameter for the number of variables randomly sampled as candidates at each split. We will assign the output of the `train` function to a variable called `model_rf`, then print and plot the model using the `print` and `plot` functions.
# Fit the random forest model model_rf <- train(Species ~ ., data = train, method = "rf", metric = "Accuracy", trControl = trainControl(method = "cv", number = 10), tuneGrid = data.frame(mtry = seq(1, 4, by = 1))) # Print the model print(model_rf) # Plot the model plot(model_rf)# this will display the prediction made by the model.

From the output, we can see that the random forest model has an accuracy of 95.83% and a kappa of 0.925, the same as the previous models. We can also see the plot of the accuracy versus the number of variables randomly sampled at each split, which shows that the accuracy does not change much as the number of variables increases.
It suggests that the random forest model is robust to the choice of the number of variables. We can also see the plot of the variable importance, which shows the relative importance of each feature for predicting the class label. The coefficients of linear discriminants reveal that the most important feature is Petal.Length, followed by Petal.Width, Sepal.Length, and Sepal.Width. This plot can help us understand which features are more influential in the classification task.
LDA vs. SVM, Trees … Which is Best?
| Model | Accuracy | Kappa | Parameters/Tuning |
|---|---|---|---|
| LDA | NA | NA | NA |
| KNN | 0.983 | 0.975 | k = 10 |
| SVM | 0.983 | 0.975 | C = 0.66 |
| Naive Bayes | 0.975 | 0.9625 | usekernel = TRUE |
| PCA | NA | NA | NA |
| Decision Tree | 0.933 | 0.9 | cp = 0.1 |
| Random Forest | 0.958 | 0.9375 | mtry = 4 |
Based on the provided results, the Support Vector Machine (SVM) model with a linear kernel appears to be the best-performing model, achieving an accuracy of 98.3% and a kappa value of 0.975. It performance is comparable to the K-Nearest Neighbors (KNN) model, which also achieved the same accuracy and kappa values. However, the SVM model achieved this performance with a single tuning parameter (C = 0.66), while the KNN model required specifying the number of neighbors (k = 10). Moreover, the SVM model demonstrates consistently high accuracy across various tuning parameter values, indicating robustness. Therefore, based on these results, the SVM model with a linear kernel is recommended for further consideration.
Conclusion
Choosing the right approach requires experience and a careful understanding of your specific data and goals. Don't leave your results to chance – let's work together to unlock the full potential of your machine-learning project. Get started with a free 30-minute Zoom meeting – let's discuss how I can optimize your classification approach.
Book Now.Frequently Asked Questions (FAQs)
What is Linear Discriminant Analysis (LDA)?
Linear Discriminant Analysis (LDA) is a method used in statistics, pattern recognition, and machine learning to find a linear combination of features that characterizes or separates two or more classes of objects or events.
How does LDA compare to other classification methods?
What are the key differences between LDA and QDA?
Linear Discriminant Analysis (LDA) assumes that the observations within each class are drawn from a multivariate Gaussian distribution with a shared covariance matrix. On the other hand, Quadratic Discriminant Analysis (QDA) assumes that each class has its unique covariance matrix, a presumption that is vital in learning algorithms for categorizing into two groups.
What are some common terms associated with classification models?
Some common terms associated with classification models include validation, training set, discriminant function, classifier, sample size, dependent variable, misclassification, predicted class, prior probabilities, regularized discriminant analysis, cross-validation, and test set.
How is the performance of LDA evaluated?
The performance of LDA is evaluated through various techniques, such as cross-validation, where the data is split into training and test sets to assess the model's ability to generalize to unseen data. Additionally, the accuracy and misclassification rates are commonly used to compare the performance of LDA with other classification methods.
Can LDA be used for binary classification?
Yes, LDA can be used for binary classification, where the goal is to assign an observation to one of two classes based on predictor variables.
What are the primary advantages of using LDA for classification?
LDA offers the advantage of dimensionality reduction while preserving the discriminatory information between classes. It also provides a clear interpretation of the discriminant function coefficients, making it useful for feature selection and understanding the influence of predictor variables on class separation.
Need a Customized solution for your data analysis projects? Are you interested in learning through Zoom? Hire me as your data analyst. I have five years of experience and a PhD. I can help you with data analysis projects and problems using R and other tools. To hire me, you can visit this link and fill out the order form. You can also contact me at info@rstudiodatalab.com for any questions or inquiries. I will be happy to work with you and provide you with high-quality data analysis services.

%20with%20Other%20classification.png)



%20with%20Other%20classification.png)