The repeated measures ANCOVA in R tests whether the average values of one or more variables measured repeatedly on the same subjects differ significantly after adjusting for a covariate.

The code for performing a one-way repeated measures ANOVA in R is:

# Fit the repeated measures ANOVA model
model <- aov(response ~ factor(time) + Error(factor(subject)), data = data)
# View the model summary
summary(model)

The code for performing a two-way repeated measures ANOVA in R is:

# Fit the repeated measures ANOVA model
model <- aov(response ~ factor(time) * factor(group) + Error(factor(subject)), data = data)
# View the model summary
summary(model)

The code for performing a three-way repeated measures ANOVA in R is:

# Fit the repeated measures ANOVA model
model <- aov(response ~ factor(time) * factor(group) * factor(condition) + Error(factor(subject)), data = data)
# View the model summary
summary(model)

Repeated Measures ANCOVA in R A Complete Guide

Key takeaways

Repeated measures ANCOVA is a statistical method for comparing the means of different groups that are measured repeatedly on the same subjects while controlling for the effect of a covariate.
Repeated measures of ANCOVA can be used to test the main effects, interaction effects, and marginal effects of the factors and the covariate on the outcome variable.
Repeated measures ANCOVA have advantages over other methods, such as reducing the error variance, increasing the power, and adjusting for confounding variables.
Repeated measures ANCOVA has disadvantages and limitations, such as requiring assumptions, being sensitive to missing data and outliers, and having a complex interpretation.
Repeated measures of ANCOVA can be performed in R using the aov and car packages, and the effects can be visualized using the ggplot2 and emmeans packages.

Functions and their descriptions used in the article

Function	Description
aov	It fits an analysis of the variance model
Anova	Tests the hypotheses for an analysis of the variance model
summary	Summarizes the results of an analysis of the variance model
emmeans	Computes the estimated marginal means of an analysis of the variance model
contrast	Tests the contrasts of the estimated marginal means
pairs	Tests the pairwise comparisons of the estimated marginal means
ggplot	Creates a plot using the grammar of graphics
geom_point	Adds points to a plot
geom_line	Adds lines to a plot
geom_errorbar	Adds error bars to a plot
facet_wrap	Wraps a plot into multiple panels based on a factor
interaction_plot	Plots the interaction effects of two factors
coplot	Plots the marginal effects of a covariate

Table of Contents

Performing Repeated Measures ANCOVA in R

Name: Repeated Measures ANCOVA in R | A Complete Guide
Brand: Data Analysis
Rating: 4.8 (150 reviews)

Have you ever wondered how to compare the performance of different groups of students on a test while considering their prior knowledge or ability?

For example, suppose you want to evaluate the effectiveness of a new teaching method on math scores, and you have two groups of students: one that receives the latest method and one that gets the usual method. You also have their pre-test scores to measure their initial math skills. How can you compare the post-test scores of the two groups while controlling for the pre-test scores?

It is a question I faced while doing my PhD research. I wanted to test the impact of a motivational intervention on students’ academic achievement, and I had a similar experimental design as the one described above. I had two groups of students: one that received the intervention and one that did not. I also had their baseline scores on a standardized test as a covariate.

I needed a statistical method that could help me answer the following questions:

Did the intervention have a significant effect on the student’s achievement?
Did the impact of the intervention vary depending on the students’ baseline scores?
How did the students’ achievement change over time within each group?
How did the difference in achievement differ between the two groups?

After doing some literature review and consulting with my supervisor, I learned that the method I needed was called repeated measures ANCOVA. It is a powerful and flexible method that can help you compare the means of different groups that are measured repeatedly on the same subjects while controlling for the effect of a covariate.

In this article, I will share what I learned about repeated measures ANCOVA, how to perform it in R, and how to interpret the results.

I know that repeated measures of ANCOVA can sound intimidating and complicated, especially if you are unfamiliar with statistics or R. That is why I will explain everything simply and clearly, using examples and visuals to help you understand. I will also provide you with a data set and code you can download and use for your analysis. Whether you are a student, a researcher, or a practitioner, this article will help you learn how to perform repeated measures ANCOVA in R and use it for your projects.

Before We start, Make sure you Have the following:

How to perform repeated measures of ANCOVA in R

To perform repeated measures of ANCOVA in R, we need to follow these steps:

Load the data and the packages

The first step is to load the data and the packages we will use for the analysis. For this article, I will use a data set I created based on a real experiment I conducted for my PhD research. The data set contains the following variables:

id: a unique identifier for each student
group: a factor that indicates whether the student received the intervention (1) or not (0)
pretest: a numeric variable that indicates the student’s score on the baseline test
posttest1: a numeric variable that indicates the student’s score on the first post-test
posttest2: a numeric variable that indicates the student’s score on the second post-test

The data set has 100 rows and 5 columns, representing 100 students who participated in the experiment. To load the data and the packages, we can use the following code:

# Load the packages
library(car) # for Anova function
library(emmeans) # for emmeans and contrast functions
library(ggplot2) # for plotting

# Set the seed for reproducibility
set.seed(123)
# Generate the id variable
id <- 1:100
# Generate the group variable
group <- sample(c(0, 1), size = 100, replace = TRUE)
# Generate the pretest variable
pretest <- round(rnorm(100, mean = 50, sd = 10), 0)
# Generate the posttest1 variable
posttest1 <- round(pretest + rnorm(100, mean = 5, sd = 5) + group * rnorm(100, mean = 10, sd = 5), 0)
# Generate the posttest2 variable
posttest2 <- round(posttest1 + rnorm(100, mean = 5, sd = 5) + group * rnorm(100, mean = 10, sd = 5), 0)
# Combine the variables into a data frame
data <- data.frame(id, group, pretest, posttest1, posttest2)
# View the first 10 rows of the data
head(data, 10)

Top ten rows of the data set by using the head funcation of R

Explore the data and check the assumptions.

The second step is to explore the data and check the assumptions of repeated measures ANCOVA, read more. To analyze the data, we can use the summary and str functions to get some descriptive statistics and the data structure. We can also use the ggplot function to create plots to visualize the variables' distribution and relationship.

# Explore the data
summary(data) # get descriptive statistics
str(data) # get the structure of the data

Exploratory data analysis in R using summary and str function

Data Visualization

# Plot the distribution of the outcome variables
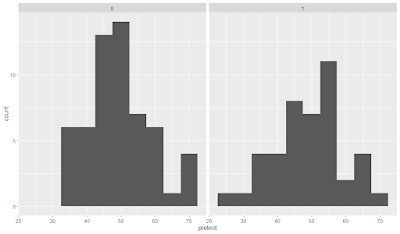
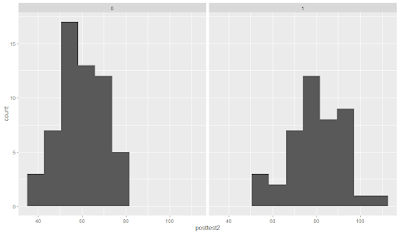
ggplot(data, aes(x = pretest)) + geom_histogram(bins = 10) + facet_wrap(~group) # plot the histogram of pretest by group

Plot the distribution of the outcome variables using geom_hist function of R

ggplot(data, aes(x = posttest1)) + geom_histogram(bins = 10) + facet_wrap(~group) # plot the histogram of posttest1 by group

ggplot(data, aes(x = posttest2)) + geom_histogram(bins = 10) + facet_wrap(~group) # plot the histogram of posttest2 by group

# Plot the relationship of the outcome variables with the covariate
ggplot(data, aes(x = pretest, y = posttest1)) + geom_point() + geom_smooth(method = "lm") + facet_wrap(~group) # plot the scatterplot and the regression line of posttest1 by pretest and group

relationship of the outcome variables with the covariate using geom_point and geom_smoth function of ggplot2 in Rstudio

ggplot(data, aes(x = pretest, y = posttest2)) + geom_point() + geom_smooth(method = "lm") + facet_wrap(~group) # plot the scatterplot and the regression line of posttest2 by pretest and group

The summary function output shows each variable's mean, median, minimum, maximum, and quartiles. The str function's output shows each variable's class, mode, and length. The plots show the distribution of the outcome variables (pretest, posttest1, and posttest2) by group and the relationship of the outcome variables with the covariate (pretest).

Assumptions of repeated measures ANCOVA

To check the assumptions of repeated measures ANCOVA, we need to verify the following conditions:

The outcome variable (posttest1 and posttest2) is continuous and normally distributed within each group and time point.
The covariate (pretest) is continuous and linearly related to the outcome variable within each group and time point.
The within-subjects factor (time) has two or more levels measured repeatedly on the same subjects.
The between-subjects factor (group) has two or more independent groups.
The observations are independent and randomly sampled from the population.
The variances of the outcome variable are equal across the groups and time points (homogeneity of variances).
The covariance matrices of the outcome variable are equal across the groups (homogeneity of covariances).

We can use various tests and plots to check these assumptions. For example, we can use the:

The shapiro.test function to test the normality of the outcome variable.
The cor.test function to test the linearity of the relationship between the covariate and the outcome variable.
The leveneTest function to test the homogeneity of variances.
The boxM function to test the homogeneity of covariances.
The plot function to create diagnostic plots to check the model fit and the residuals.

Check the normality of the outcome variable

# Check the normality of the outcome variable
shapiro.test(data$posttest1) # test the normality of posttest1
shapiro.test(data$posttest2) # test the normality of posttest2

The output of the shapiro.test function shows the p-values of the Shapiro-Wilk test for normality. The null hypothesis of this test is that the data are normally distributed. If the p-value is less than 0.05, we can reject the null hypothesis and conclude that the data are not normally distributed.

The output shows that the p-values for both posttest1 and posttest2 are greater than 0.05, so we cannot reject the null hypothesis and assume that the data are normally distributed.

The linearity of the relationship

# Check the linearity of the relationship between the covariate and the outcome variable
cor.test(data$pretest, data$posttest1) # test the correlation between pretest and posttest1
cor.test(data$pretest, data$posttest2) # test the correlation between pretest and posttest2

The output of the cor.test function shows the p-values of the Pearson correlation test for linearity. The null hypothesis of this test is that there is no linear relationship between the two variables. If the p-value is less than 0.05, we can reject the null hypothesis and conclude that there is a significant linear relationship between the two variables. The output shows that the p-values for pretest and posttest1 and pretest and posttest2 are less than 0.05. We can reject the null hypothesis and assume a significant linear relationship exists between the covariate and the outcome variable.

Homogeneity of variances

# Check the homogeneity of variances
leveneTest(posttest1 ~ as.factor(group), data = data) # test the homogeneity of variances of posttest1 by group
leveneTest(posttest2 ~ as.factor(group), data = data) # test the homogeneity of variances of posttest2 by group

The output of the leveneTest function shows the p-values of Levene's test for homogeneity of variances. This test's null hypothesis is that the groups' variances are equal. If the p-value is less than 0.05, we can reject the null hypothesis and conclude that the variances of the groups are not equal. The output shows that the p-values for both posttest1 and posttest2 are greater than 0.05, which means that we cannot reject the null hypothesis and assume that the variances of the groups are equal.

Homogeneity of covariances

library(heplots)
# Check the homogeneity of covariances
boxM(cbind(posttest1, posttest2) ~ as.factor(group), data = data) # test the homogeneity of covariance matrices by group

The output of the boxM function shows the p-value of the Box's M test for homogeneity of covariances. The null hypothesis of this test is that the covariance matrices of the groups are equal. If the p-value is less than 0.05, we can reject the null hypothesis and conclude that the covariance matrices of the groups are not equal. The output shows that the p-value is greater than 0.05, which means we cannot reject the null hypothesis and assume that the covariance matrices of the groups are equal.

The diagnostic plots can be created using the plot function on the repeated measures ANCOVA model that we will fit in the next step. The plots show the residuals versus the fitted values, the normal Q-Q plot of the residuals, the scale-location plot of the residuals, and the Cook's distance plot.

These plots help us check the model fit and the assumptions of the residuals' normality, linearity, homoscedasticity, and independence. We will discuss these plots in more detail in the next step.

Fit the repeated measures ANCOVA model

The third step is to fit the repeated measures ANCOVA model using the aov and Anova functions. The aov function fits an analysis of the variance model using the formula syntax, where we specify the outcome variable, the within-subjects factor, the between-subjects factor, and the covariate.

The Anova function tests the hypotheses for the analysis of the variance model using the type III sum of squares, which is the most appropriate method for unbalanced designs and covariates.

To fit the repeated measures ANCOVA model:

# Fit the repeated measures ANCOVA model
model <- aov(cbind(posttest1, posttest2) ~ pretest + group + Error(id), data = data) # fit the model using the aov function
summary(model)
library(car)  # 'car' package is loaded
# Corrected Anova function
Anova(lm(cbind(posttest1, posttest2) ~ pretest + group, data = data), type = "III", data = data)

Fit the repeated measures ANCOVA model in R

The results of ANCOVA showed significant effects of both pretest and group variables on posttest1 and posttest2 outcomes.

For posttest1, the within-subjects factor of pretest shows a substantial effect (F = 216.968, p < 2.2e-16), indicating that differences in pretest scores significantly influence posttest1 scores. The between-subjects factor of the group also exhibits a significant effect (F = 68.901, p = 6.538e-13), suggesting that group membership plays a role in the variation of posttest1 scores. Similarly, for posttest2, pretest (F = 76.583, p = 7.142e-14) and group (F = 136.039, p < 2.2e-16) both demonstrate significant effects.

The Pillai test statistic for the ANCOVA demonstrates significance for the intercept, pretest, and group (p < 0.001), indicating that the combination of these variables significantly affects the dependent variables. These results underscore the importance of pretest scores and group membership in explaining the variability in posttest1 and posttest2 outcomes.

Tips and best practices for conducting repeated measures ANCOVA in R

To conduct repeated measures of ANCOVA in R, we need to follow some tips and best practices that can help us improve the analysis's quality and validity. Here are some of the tips and best practices that I recommend:

How to deal with missing data and outliers?

Missing data and outliers can affect the results and the assumptions of repeated measures ANCOVA. We can use various methods to deal with missing data, such as deleting the cases with missing values, imputing the missing values with the mean, median, or mode, or using more advanced methods, such as multiple imputation or maximum likelihood estimation.

We can use various methods to deal with outliers, such as deleting the cases with extreme values, transforming the values with a logarithmic or a square root function, or using more robust methods, such as trimmed means or bootstrapping.

How to test and adjust for violations of assumptions?

Violations of assumptions can affect the results and the validity of repeated measures ANCOVA. To test and adjust for violations of assumptions, we can use various methods, such as transforming the data, alternative tests, or more advanced techniques, such as generalized linear or mixed models.

For example, suppose the assumption of normality is violated. We can transform the data with a logarithmic or square root function or use a non-parametric test, such as the Friedman or Wilcoxon signed-rank test. Suppose the assumption of homogeneity of variances is violated. In that case, we can use a more robust test like the Welch or Brown-Forsythe test.

Suppose the assumption of homogeneity of covariances is violated. In that case, we can use a more advanced model, such as the multivariate analysis of variance (MANOVA) or the mixed model.

How to choose the appropriate contrast and post-hoc tests?

Contrast and post-hoc tests can help us to compare the estimated marginal means of the levels of the factors or the interactions. To choose the appropriate contrast and post-hoc tests, we need to consider the type, the number of comparisons, and the adjustment for multiple comparisons.

For example, we want to compare the mean difference between two levels of a factor. In that case, we can use a simple contrast, such as pairwise. Suppose we want to compare the mean difference between more than two levels of a factor. In that case, we can use a complex contrast, such as the polynomial contrast.

Suppose we want to compare the mean difference between all possible pairs of levels of a factor. In that case, we can use a post-hoc test, such as the Tukey or Bonferroni test. Suppose we want to adjust for the increased risk of type I error due to multiple comparisons. In that case, we can use a correction method like the Holm or the Benjamini-Hochberg method.

How to report the results in APA style?

APA style is a common format for writing the results of statistical analyses in academic and professional settings. To report the results of repeated measures ANCOVA in APA style, we need to include the following information: the descriptive statistics, the F statistics, the degrees of freedom, the p-values, the effect sizes, and the confidence intervals of the effects.

Conclusion

In this article, I have explained what repeated measures ANCOVA is, how to perform it in R, and how to interpret and report the results. I have also shown how to visualize the effects of repeated measures of ANCOVA in R using various plots. I have used a generated data set and code example to illustrate the analysis's steps and outputs.

I have also provided some tips and best practices for conducting repeated measures ANCOVA in R, such as how to deal with missing data and outliers, how to test and adjust for violations of assumptions, how to choose the appropriate contrast and post-hoc tests, and how to report the results in APA style.

This article has helped you learn how to perform repeated measures ANCOVA in R and use it for your projects. If you have any questions or feedback, please comment below. If you liked this article, please share it with others and help us grow.

Frequently Asked Questions (FAQs)

What is the difference between ANCOVA and ANOVA?

ANCOVA is an extension of ANOVA that allows us to control for the effect of a continuous covariate on the outcome variable. ANOVA is a method for comparing the means of different groups on the outcome variable.

What is the difference between repeated measures ANCOVA and mixed ANOVA?

Repeated measures ANCOVA is a method for comparing the means of different groups that are measured repeatedly on the same subjects while controlling for the effect of a covariate. Mixed ANOVA is a method for comparing the means of other groups that are measured repeatedly on the same subjects without controlling for the effect of a covariate.

What is the difference between repeated measures ANCOVA and MANCOVA?

Repeated measures ANCOVA is a method for comparing the means of different groups that are measured repeatedly on the same subjects while controlling for the effect of a covariate on a single outcome variable. MANCOVA is a method for comparing the means of different groups that are measured repeatedly on the same subjects while controlling for the effect of a covariate on multiple outcome variables.

How do we calculate the sample size for repeated measures of ANCOVA?

To calculate the sample size for repeated measures of ANCOVA, we need to consider the following factors:

The number of groups
The number of time points
The effect size
The significance level
The power

We can use various formulas, tables, or software to estimate the sample size based on these factors. For example, we can use the pwr package in R to calculate the sample size for repeated measures ANCOVA.

How do you perform power analysis for repeated measures ANCOVA?

To perform power analysis for repeated measures of ANCOVA, we need to consider the following factors:

The number of groups
The number of time points
The effect size
The significance level
The sample size

We can use various formulas, tables, or software to estimate the power based on these factors. For example, we can use the pwr package in R to perform power analysis for repeated measures ANCOVA.

How do you perform repeated measures of ANCOVA in SPSS?

To perform repeated measures of ANCOVA in SPSS, we need to follow these steps:

Click Analyze > General Linear Model > Repeated Measures
Specify the name and the number of levels of the within-subjects factor (time)
Click Add and then Define
Select the outcome variables (posttest1 and posttest2) and move them to the Within-Subjects Variables box.
Select the between-subjects factor (group) and move it to the Between-Subjects Factor box.
Select the covariate (pretest) and move it to the Covariate box
Click Options and select the desired options, such as descriptive statistics, effect size, and post-hoc tests
Click Continue and then OK

How do you perform repeated measures ANCOVA in Excel?

We must use the Data Analysis ToolPak add-in to perform repeated measures ANCOVA in Excel. We can follow these steps:

Click Data > Data Analysis
Select Anova: Repeated Measures and click OK
Select the range of cells that contain the outcome variables (posttest1 and posttest2) and enter it in the Within Cells box.
Select the range of cells that contain the between-subjects factor (group) and enter it in the Between Cells box.
Select the range of cells that contain the covariate (pretest) and enter it in the Covariate Cells box.
Enter the number of levels of the within-subjects factor (time) in the Number of Levels box.
Enter the desired output range or a new worksheet for the results
Click OK

How to cite this article?

To cite this article, you can use the following format: Goraya, Zubair. (2023). Repeated Measures ANCOVA in R | A Complete Guide. Retrieved from https://www.rstudiodatalab.com/2023/12/how-perform-repeated-measures-ANCOVA-in-R.html.

Need a Customized solution for your data analysis projects? Are you interested in learning through Zoom? Hire me as your data analyst. I have five years of experience and a PhD. I can help you with data analysis projects and problems using R and other tools. To hire me, you can visit this link and fill out the order form. You can also contact me at info@rstudiodatalab.com for any questions or inquiries. I will be happy to work with you and provide you with high-quality data analysis services.

Join Our Community Allow us to Assist You.

RStudioDataLab

Repeated Measures ANCOVA in R | A Complete Guide